(Note: this post was updated on 2024-02-02 with additional content)

What are NeRFs?

NeRF stands for Neural Radiance Fields, and is a method for optimizing a continuous, differentiable, volumetric representation of a scene, from which novel views can be synthesized. That's quite a hefty description, but don't worry, I'll break it down piece by piece in this post.

Why do I care?

The potential applications of NeRFs are pretty wide. Compared to previous methods, they can generate extremely high-quality 3D reconstructions of a scene, with relatively few input images. And once you have a trained model, you can generate an image/view from anywhere in that scene! On top of the reconstructed scene, you can also place newly generated object, giving way to augmented reality type applications, which could be useful for metrology, medical imaging, or just plain fun in video games. Beyond this, researchers in the field of robotics are also using NeRFs to generate 3D models an environment, which they can subsequently use for planning and trajectory generation.

Below are two examples of NeRFs in action, where the first is a NeRF of a robotics lab, and the second is a NeRF of an excavator scene. You can see that the quality of the generated views is quite high, and with recent optimization and improvements made to the original NeRF architecture, the time to train the models that generate this scene is only a few minutes!

Instant NGP NeRF — A NeRF of a robotics lab: Credits to Instant-NGP

Excavator NeRF — A NeRF of an excavator scene: Credits to Nvidia

Novel View Synthesis

Novel view synthesis is a term used to describe the generation of a view (or image less formally), from a pose (a position and orientation in space) that has not been explicitly seen before.

Volumetric Reprentation

To generate a novel 2D views, we must have some 3D representation of the scene. In the case of NeRFs, this is done by representing the scene as a neural network. More specifically, a fully-connected (FC) network, which has a 5D input ($x, y, z, \theta, \phi$) and outputs a 4D vector ($r, g, b, \sigma$). Here ($x, y, z$) are the 3D coordinates of a point in the scene, and ($\theta, \phi$) are the angles of the ray that points along. For the outputs, ($r, g, b$) are the pixel values of the point, and $\sigma$ is the estimated density of the point.

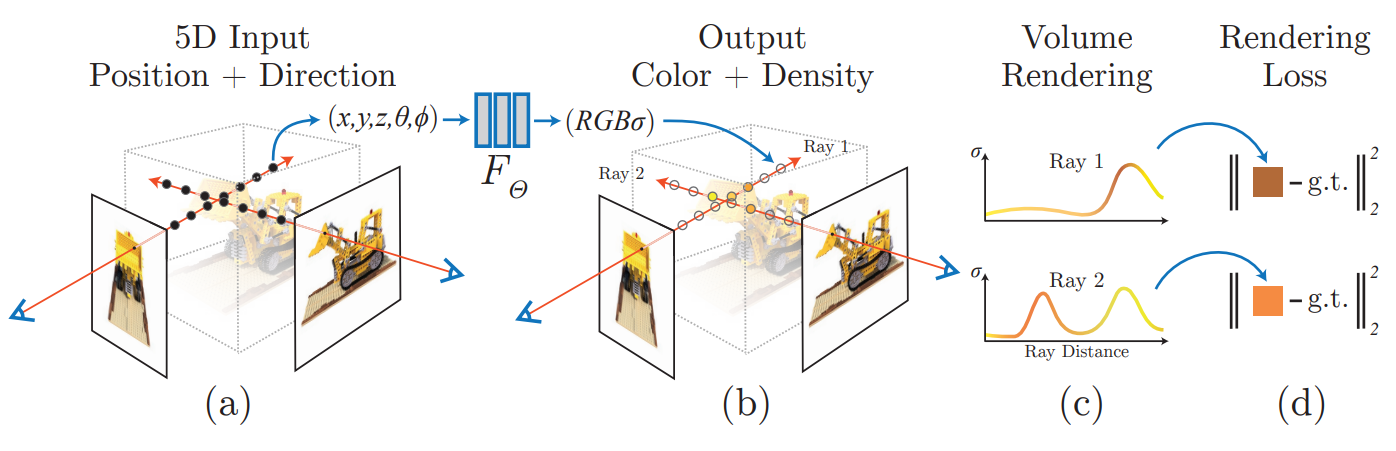
Nerf Process Visualization — An overview of the NeRF training and generation process. Credits to the original NeRF paper [2]

The key here is that because this representation is a fully-connected neural network, it is continuous and differentiable, allowing for the optimization of the scene.

Walking Through the Pipeline

Training

Input Data

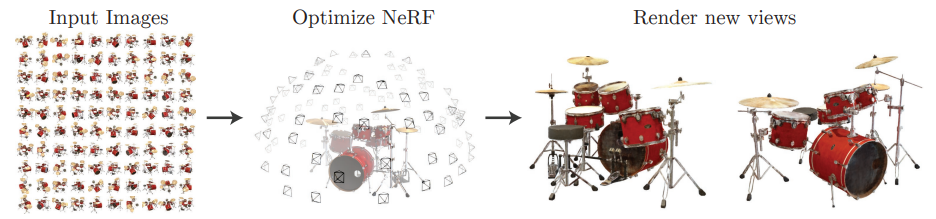
A general requirement of the input data for Vanilla NeRF models is that you have a set of images that have coverage of the scene/object to be reconstructed, and for each image you have the camera intrinsic and extrinsic parameters.

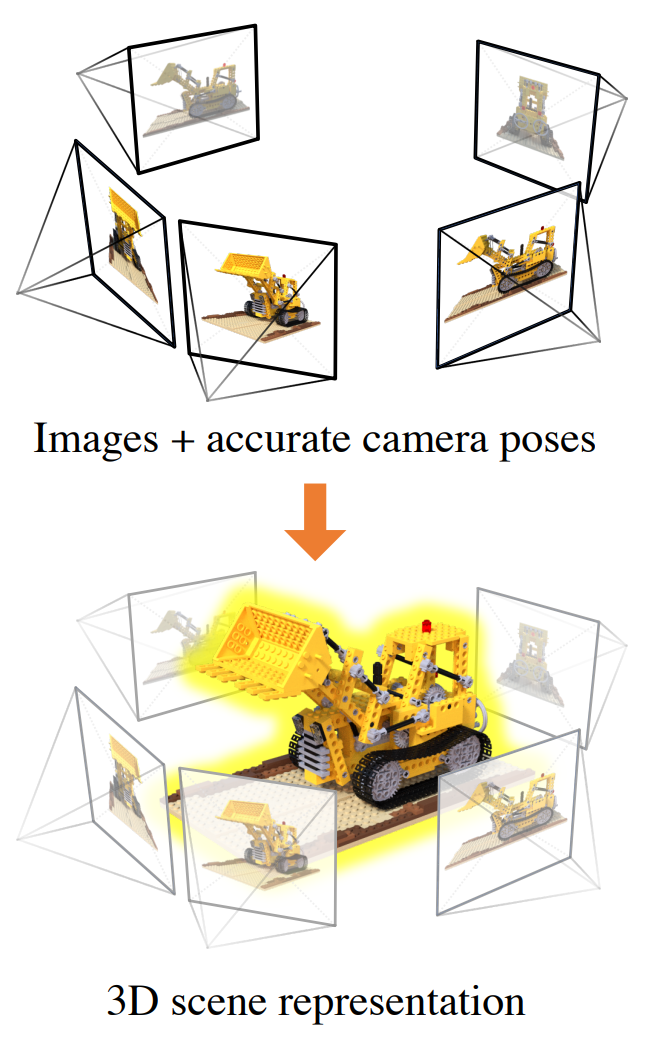
Camera Extrinsics Visualization — A visualization of the camera poses/extrinics in a scene. Credits to the BARF paper

With this dataset, you then randomly sample tuples, (image, camera_intrinsic, camera_extrinsic), for each training iteration.

Ray Generation

With a single sample tuple, the next step is generating rays from the camera intrinsics and extrinsics, which can be done analytically. Steps:

First we show the individual components that make-up the homogeneous transform of the camera extrinsics: $$T_{camera} = \begin{bmatrix}R_{camera} & t_{camera}\\0 & 1\end{bmatrix}$$ where $T_{camera}$ is the transformation matrix from camera-to-world frame, $R_{camera}$ is the rotation matrix and $t_{camera}$ is the translation vector.
The ray origin can be simply extracted from the camera extrinisics, where the translation term is considered as the center of the camera $$r_o = t_{camera} $$
Next, to simplify, we will take a single arbitrary pixel from a sample image we assume to be square (i.e. aspect ratio is 1:1) and generate a ray. Let's say this pixel has coordinates ($x_{pixel}, y_{pixel}$) in the image.
We can then use the camera intrinsics to convert the pixel coordinates to a raw ray direction, in the camera frame, which is a vector ($x_{dir}, y_{dir}, z_{dir}$) that points from the camera origin to the pixel, using the following equations: $$x_{dir} = {x_{pixel}-0.5*W \over f_x}$$ $$y_{dir} = {-(y_{pixel}-0.5*H) \over f_y}$$ $$z_{dir} = -1$$ $$r_d = (x_{dir}, y_{dir}, z_{dir})$$ Where $W$ and $H$ are the width and height of the image, and $f_x$ and $f_y$ are the focal lengths.
Then we can rotate the ray directions from the camera frame to the world frame using the camera extrinsics: $$r'_d = R_{camera} r_d $$
Finally we can normalize the ray direction as a unit vector by normalizing the vector: $$r_{d_{norm}} = {r'_d \over \lVert r'_d \rVert }$$

Following these steps for every pixel in an image, we can generate a set of rays that point from the camera origin into the scene.

A great follow up reference is this article that provides a more in depth explanation of the ray generation process.

Ray Sampling

The next step is to sample discrete points along the the generated rays, through volumetric ray-marching. The figure below displays a visualization of a single ray naively being marched through a scene from the camera's perspective.

This is a rich topic that has been explored deeply long before the creation of NeRFs, and the original NeRF authors note that their initial method of hierarchical volume sampling was inspired by previous work in volume rendering [2].

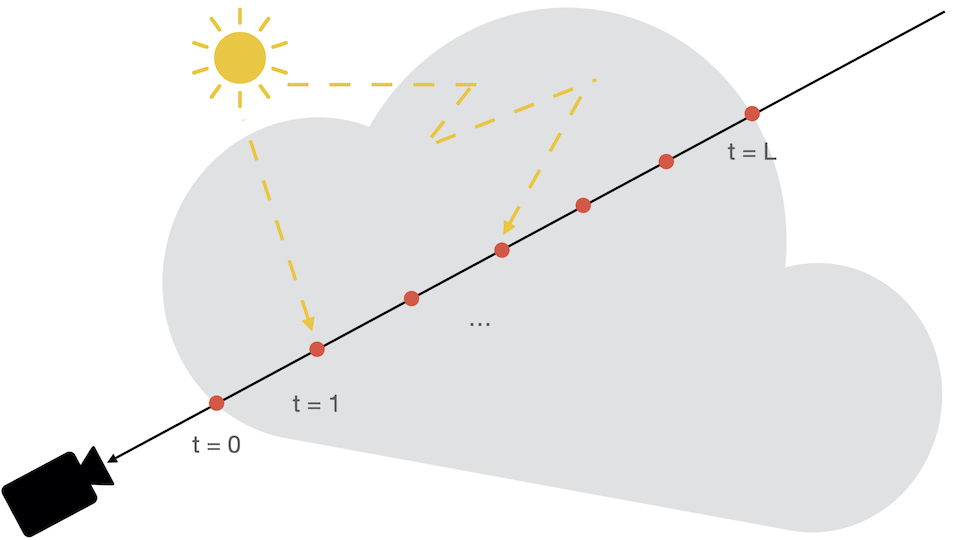
The need for a ray sampling strategy boils down to the ineffiency in naively sampling uniformly spaced points along a ray. In most scenes, a large portion of the space is empty, so time spent evaluating points in empty space is time wasted. In addition, this limits the resolution of the representation due to evaluating at fixed discrete locations [2]. To mitigate this, sampling strategies are effectively trying to build and leverage a model that estimate where points that affect the final rendering are, and sample from those locations.

I plan to expand upon a few more recent methods in this area that have shown success in NeRFs in future posts, but for now, I will give an overview of the method proposed in the original paper, as a baseline.

The method proposed in the original NeRF work was a two-step, coarse-to-fine, sampling approach, where there are two networks that represent the scene. This method starts with performing stratified sampling where each ray is partitioned into N evenly-spaced bins between $[t_n, t_f]$, where $t_n$ is a minimum distance from the origin to sample from, and $t_f$ is the maximum. The samples are then drawn uniformly from each bin according to this equation [2]: $$t_i \sim \mathcal{U}\left[t_n + \frac{i-1}{N}(t_f - t_n), t_n + \frac{i}{N}(t_f - t_n)\right]$$

Stratified Sampling Example — An example of stratified sampling, and demonstrated by uedufy

The points from the stratified sampling strategy are used as the inputs to evaluate the coarse network. The output of the coarse network is then used to create a probability density function (PDF) along the ray that can be sampled and used as input to the fine-network.

NeRF Function Representation and Training

To represent the scene we seek to generate novel views from, the representation is formulated as a function that takes in an input vector containing a position and direction, and outputs an RGB color value and associated density. In the original work, they formulate the input as a 5D vector, with position represented as ($x, y, z$), and the direction represented with angles ($\theta, \phi$), but they note that in practice the viewing direction is instead represented as unit-vector ($x_{dir}, y_{dir}, z_{dir}$), making the input 6D [2].

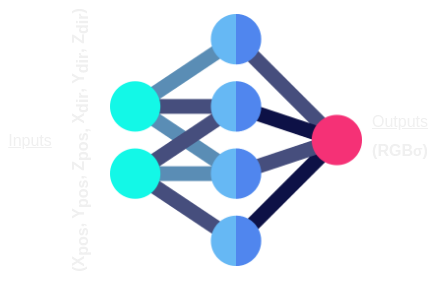
NeRF MLP Network — Visualization of the inputs and outputs of a NeRF MLP

The function described above is a Multi-Layer-Perceptron (MLP), or a neural-network that only contains fully-connected (FC) layers. Referring back to the volume rendering techniques described at the beginning of thie post, since the process is differentiable, we can optimize the parameters of the MLP described to minimize the error between the pixel values of the images in our input data and the pixel values of the generated views output from the MLP, as shown by the MSE loss below: $$\mathcal{L}_{MSE} = \frac{1}{N}\sum_{i=1}^{N} ( I_{gt} - I_{pred})^2$$ Where $I_{gt}$ is the ground truth image, $I_{pred}$ is the predicted image, and $N$ is the number of pixels in the image.

Rendering Novel Views

Once the NeRF has been trained, generating novel views is as simple as passing the pose of the desired view to the NeRF, and taking the output as the RGB pixel values. If the input dataset contains enough coverage of the scene, the NeRF should be able to generate high-quality views from any nearby pose.

Putting it All Together

To summarize, the process of training a NeRF involves looping through the following steps:

Generating rays from the camera intrinsics and extrinsics
Sampling significant points along rays from those generated (and subsequently updating the density estimation along a ray)
Passing those points through the NeRF to get the RGB and sigma values output from the neural network radiance field approximation function
Comparing the RGB and sigma values to the ground truth image with an MSE loss function
Backpropagating the loss through the NeRF to update the neural network weights, and repeating until some stopping criteria is met
Running interference on the trained model, and rendering novel views from the scene

Flow of NeRF Training and Generation — An overview of the flow of training and generating with NeRFs (taken from original paper [2])

How can I get started with NeRFs?

The best route to go down here is really determined by how deep you want to go. If you're just interested in using NeRFs, and you have some general computing knowledge, there are many open source projects that you can use to generate NeRFs. If you're interested in understanding the theory and implementation of NeRFs, I discuss that in the following sections as well.

Reading Papers and Code

My first recommendation is to read the original paper, which is very digestable and well written. In parallel, I recommend to also reference the code the authors have released alongside the paper, and attempt to draw the connections between the code a paper. Many important aspects are always left as "implementation details" in papers, and the only way to extract them is to read through the code!

Other methods I highly recommend people read through is Instant-NGP, DeRF, Mip-NeRF, and NeuS, likely in that order. Each one of these papers has a unique contribution to the field, and shows that this first paper just ignited a fire of awesome research in the field.

Building and Experimenting

I truly believe the only real way to understand a technical topic like this is to get your hands dirty and work through an implementation. Start with trying to implement the Vanilla NeRF model, and then work your way through adding new methods, tuning hyperparameters, and getting a feel for what affects the outputs of the pipeline.

There are some awesome libraries out there for building and experimenting with NeRFs. Here are a few:

NerfAcc - This is a library that contains implementations of common ray sampling and volume rendering strategies that are common to almost all NeRF implementations.
NerfStudio - A library that contains a full pipeline for training NeRFs, using existing implementations, and also has a GUI for visualizing the process.
Awesome-NeRF - A collection of NeRF resources and papers on different methods

Cool Applications!

The community is building so many cool things with NeRFs -- here are a few examples of what's out there:

NeRFs in Robotics - A repo showing NeRFs being used for performing Simultanous Localization and Mapping (SLAM) for robot navigation
Instruct-NeRF2NeRF - A method for editing a scene by adding new objects to a NeRF through a text prompt by integrating LLMs

References

A huge shoutout to the producers of the following repos/papers/blog posts, which I used to help me write this post:

Intro to NeRFs